Site navigation:

Elementary tutorial: A 1D discrete mapping (the Lorenz map)

See Tutorial_LorenzMap.py.

A 1D mapping can be derived from an approximation to the triple-zero unfolding of the Lorenz system of ODEs (e.g., see the original XPP tutorial example):

\( z(t+1) = a+b (z(t)-c)^2, \quad \) (Lor)

where t is discrete time. To define the Lyapunov exponent we follow the linearization of Eq. (Lor) along its solutions in log coordinates, namely , and look at the long term behavior of , which is an 'auxiliary' value derived from the map varible zp (the same way that auxiliary variables are defined in XPP.).

The system is specified using PyDSTool with 


import PyDSTool as dst
from PyDSTool import args
import numpy as np
from matplotlib import pyplot as plt

DSargs = args(name='Lorenz map')
DSargs.varspecs = {'z': 'a+b*(z-c)**2',   # note syntax for power
                   'zp': 'zp+log(abs(2*b*(z-c)))',
                   'L': 'zp/(t+1)'}  # L is an auxiliary variable
DSargs.tdomain = [0, 200]            # Default range of independent variable 't' 
DSargs.pars = args(a=2.93,
                   b=-1.44,
                   c=1.85)           # Using args() class to specify parameters with less syntax than a dictionary
DSargs.vars = ['z', 'zp']            # Implicitly, then, L will be an auxiliary variable
DSargs.ics = {'z': 2, 'zp': 0}       # Initial conditions
DSargs.ttype = int                   # force independent variable type to be integer (discrete time)

Notice that the variable L is defined using t+1 because the discrete time begins at 0.

Solutions

The solution of the discrete dynamical system Eq. (Lor) can be computed using a Generator mapping instance: 


lmap = dst.Generator.MapSystem(DSargs)   # an instance of the 'Generator' class for maps.
traj = lmap.compute('test')              # compute a trajectory named 'test'
pts = traj.sample()                      # sample the points from the trajectory

# PyPlot commands
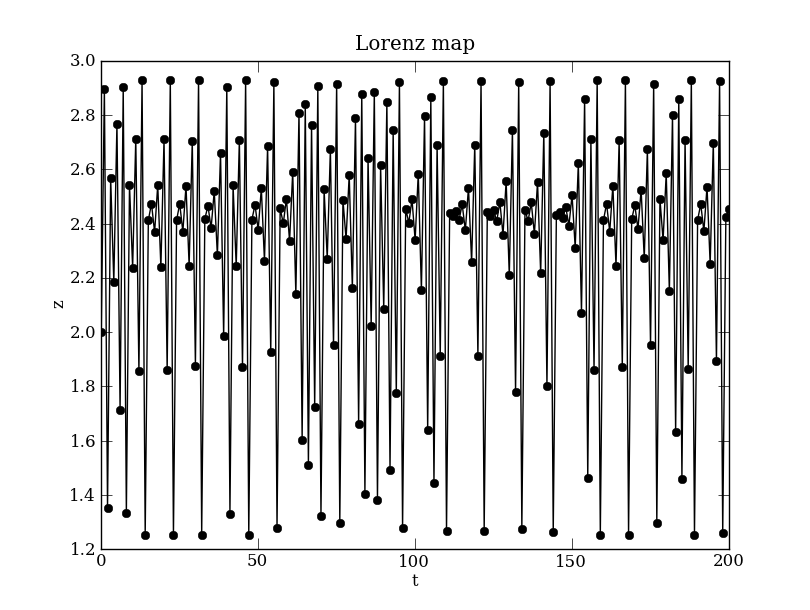
plt.figure(1)
plt.plot(pts['t'], pts['z'], 'ko-')
plt.title(lmap.name)
plt.xlabel('t')
plt.ylabel('z')

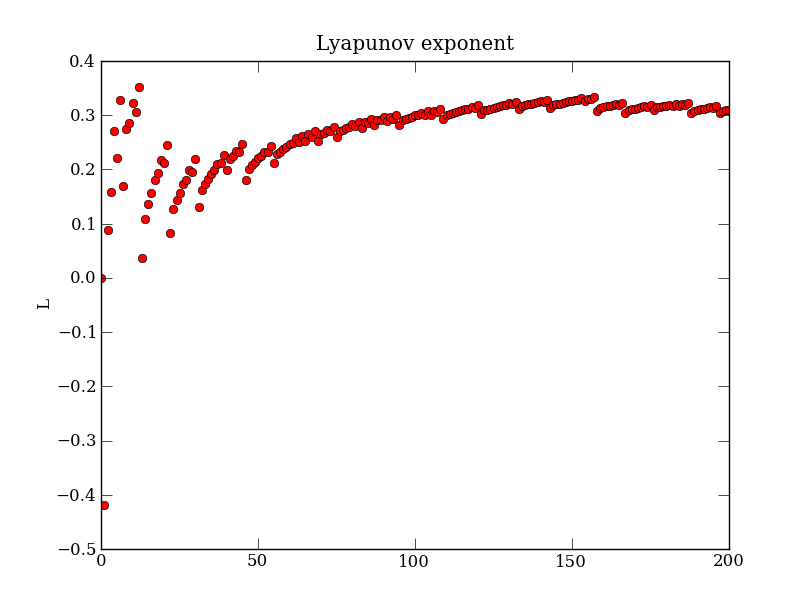
plt.figure(2)
plt.plot(pts['t'], pts['L'], 'ro')
plt.title('Lyapunov exponent')
plt.ylabel('L')
plt.xlabel('t')
plt.show()

Depending on your local configuration of the Matplotlib interactive mode, the last command plt.show() might not be necessary.